Openssl Generate Ecdh Key Pair

Posted on 15.12.202022.08.2017by admin

Openssl Generate Keypair
Openssl Generate Ecdh Key Pair Key

Please delete colons ':' and new lines for the private key and the public key and fill 'EC private key (hex)' and 'EC public key (hex)' in above form and choose proper. This program demonstrates how to generate elliptic curve cryptography (ECC. The example 'C' program eckeycreate.c demonstrates how to generate elliptic curve cryptography (ECC) key pairs, using the OpenSSL library functions. The program will create and display a new elliptic curve cryptography (ECC) key pair, similar to the output shown. Upon client receive this message it will send ClientVerifiy matched with ssl3sendclientkeyexchange. And in case of ECDH(E) openssl generate key pair using ECKEYgeneratekey (not engine's genkey) As you can see the patch: 'ecdhepatch.diff' you add ECDHgeneratekey function in server key exchange to accelerate computation. $ openssl rsa -pubout -in privatekey.pem -out publickey.pem writing RSA key A new file is created, publickey.pem, with the public key. It is relatively easy to do some cryptographic calculations to calculate the public key from the prime1 and prime2 values in the public key file. However, OpenSSL has already pre-calculated the public key.

Elliptic Curve Diffie Hellman (ECDH) is an Elliptic Curve variant of the standard Diffie Hellman algorithm. See Elliptic Curve Cryptography for an overview of the basic concepts behind Elliptic Curve algorithms.

Generating Public and Private Keys with openssl.exe To perform the following actions for Windows or Linux, you must have OpenSSL installed on your system. Generating the Private Key - Windows. Oct 09, 2019 How to Generate & Use Private Keys using OpenSSL's Command Line Tool These commands generate and use private keys in unencrypted binary (not Base64 “PEM”) PKCS#8 format. The PKCS#8 format is used here because it is the most interoperable format when dealing with software that isn't based on OpenSSL.

ECDH is used for the purposes of key agreement. Suppose two people, Alice and Bob, wish to exchange a secret key with each other. Alice will generate a private key d_A and a public key Q_A=d_AG (where G is the generator for the curve). Similarly Bob has his private key d_B and a public key Q_B=d_BG. If Bob sends his public key to Alice then she can calculate d_AQ_B=d_Ad_BG. Similarly if Alice sends her public key to Bob, then he can calculate d_bQ_A=d_Ad_BG. The shared secret is the x co-ordinate of the calculated point d_Ad_BG. Any eavesdropper would only know Q_A and Q_B, and would be unable to calculate the shared secret.

Using ECDH in OpenSSL[edit]

In order for two peers to exchange a shared secret they need to first agree on the parameters to be used. In Elliptic Curve Cryptography this is typically done through the use of named curves. A named curve is simply a well defined and well known set of parameters that define an elliptic curve. OpenSSL has support for a wide variety of different well known named curves. /x-509-certificate-pem-format-and-private-key-generator.html. In the example below the ANSI X9.62 Prime 256v1 curve is used.

The example below shows how to set up the parameters based on the use of a named curve, how to generate a public/private key pair for those parameters and subsequently how to derive a shared secret. The details of how to obtain the other party's key (the peer key) are omitted, as this is specific to your particular situation. Note that you do not necessarily need to generate a new private/public key pair for every exchange (although you may choose to do so). Also note that the derived shared secret is not suitable for use directly as a shared key. Typically the shared secret is passed through some hash function first in order to generate a key.

See below for the example code.

You should also refer to the EVP Key Agreement page for general information on the key agreement API in OpenSSL.

Using the Low Level APIs[edit]

Users of the OpenSSL library are expected to normally use the EVP method for working with Elliptic Curve Diffie Hellman as described above and on the EVP Key Agreement page. The EVP API is implemented by a lower level ECDH API. In some circumstances, expert users may need to use the low level API. This is not recommended for most users. However, if you need to use this then an example of use is shown below.

Openssl Generate Keypair

As noted in the high level EVP section of this page, you should never use a shared secret directly. It must be passed through some form of key derivation function (KDF) first. The last argument to ECDH_compute_key can optionally pass a function pointer for such a KDF. The shared secret will then be passed through this function and the value returned in the output buffer will be suitable for direct use as a key.

The function below is taken from apps/speed.c in the OpenSSL codebase, and shows an example of a KDF based on the hash function SHA1.

SHA1 may not be appropriate if the key length required is longer than the number of bits provided as output from the hash function. A standards based KDF which can be used to derive longer keys is described in: http://www.secg.org/collateral/sec1.pdf (see section 3.6.1)

ECDH and Named Curves[edit]

If you want to save a key and later load it with SSL_CTX_use_PrivateKey_file, then you must set the OPENSSL_EC_NAMED_CURVE flag on the key. You do that by calling EC_KEY_set_asn1_flag(ecKey, OPENSSL_EC_NAMED_CURVE). Failure to do so will result in a SSL error of 0x1408a0c1 (no shared cipher) at the server.

As an example, the following creates a elliptic curve key and saves it using a named curve rather than an expanded list of group paramters:

If you want to detect the flags after reading a key or certificate from disk, then use the following code:

The certificates below were dumped with openssl x509 -in server-ecdsa-cert.pem -text -noout. The certificate on the left was created with a key using OPENSSL_EC_NAMED_CURVE, while the certificate on the right was not. Notice the certificate on the left includes ASN1 OID: prime256v1. The certificate on the left can be used with SSL server using ECDSA, but the certificate on the right cannot because it will result in 0x1408a0c1 at the server.

Figure 1: Key with OPENSSL_EC_NAMED_CURVE

Figure 2: Key without OPENSSL_EC_NAMED_CURVE

If you use a key or certificate without without the OPENSSL_EC_NAMED_CURVE flag (i.e., one that looks like the image on the right), then the SSL connection will fail with the following symptoms:

Openssl Generate Ecdh Key Pair Key

Note that OpenSSL's X509_verify, X509_verify_cert, SSL_CTX_check_private_key, SSL_CTX_use_PrivateKey_file, and SSL_CTX_use_certificate_chain_file will not return a failure when using a key or certificate in the wrong format.

See also[edit]

Retrieved from 'https://wiki.openssl.org/index.php?title=Elliptic_Curve_Diffie_Hellman&oldid=1558'

< Cryptography

Download and install the OpenSSL runtimes. If you are running Windows, grab the Cygwin package.

OpenSSL can generate several kinds of public/private keypairs.RSA is the most common kind of keypair generation.^[1]

Other popular ways of generating RSA public key / private key pairs include PuTTYgen and ssh-keygen.^[2]^[3]

Generate an RSA keypair with a 2048 bit private key[edit]

Execute command: 'openssl genpkey -algorithm RSA -out private_key.pem -pkeyopt rsa_keygen_bits:2048'^[4] (previously “openssl genrsa -out private_key.pem 2048”)

e.g.

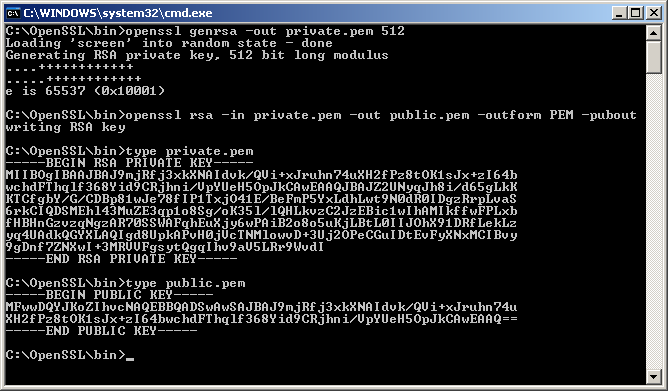
Make sure to prevent other users from reading your key by executing chmod go-r private_key.pem afterward.

Extracting the public key from an RSA keypair[edit]

Execute command: 'openssl rsa -pubout -in private_key.pem -out public_key.pem'

e.g.

A new file is created, public_key.pem, with the public key.

It is relatively easy to do some cryptographic calculations to calculate the public key from the prime1 and prime2 values in the public key file.However, OpenSSL has already pre-calculated the public key and stored it in the private key file.So this command doesn't actually do any cryptographic calculation -- it merely copies the public key bytes out of the file and writes the Base64 PEM encoded version of those bytes into the output public key file.^[5]

Viewing the key elements[edit]

Execute command: 'openssl rsa -text -in private_key.pem'

All parts of private_key.pem are printed to the screen. This includes the modulus (also referred to as public key and n), public exponent (also referred to as e and exponent; default value is 0x010001), private exponent, and primes used to create keys (prime1, also called p, and prime2, also called q), a few other variables used to perform RSA operations faster, and the Base64 PEM encoded version of all that data.^[6](The Base64 PEM encoded version of all that data is identical to the private_key.pem file).

Password-less login[edit]

Often a person will set up an automated backup process that periodically backs up all the content on one 'working' computer onto some other 'backup' computer.

Because that person wants this process to run every night, even if no human is anywhere near either one of these computers, using a 'password-protected' private key won't work -- that person wants the backup to proceed right away, not wait until some human walks by and types in the password to unlock the private key.Many of these people generate 'a private key with no password'.^[7]Some of these people, instead, generate a private key with a password,and then somehow type in that password to 'unlock' the private key every time the server reboots so that automated toolscan make use of the password-protected keys.^[8]^[3]

conf1rmed.netlify.app