Rsa Generate Key Code Openssl
- Rsa Generate Key Code Openssl Update
- Rsa Generate Key Code Openssl Pdf
- Openssl Generate Rsa Certificate
- Openssl Generate Rsa Private Key
How to generate keys in PEM formatusing the OpenSSL command line tools?
RSA keys
Getting the public key corresponding to a particular private key, through the methods provided for by OpenSSL, is a bit cumbersome. An easier way to do it is to use phpseclib, a pure PHP RSA implementation.
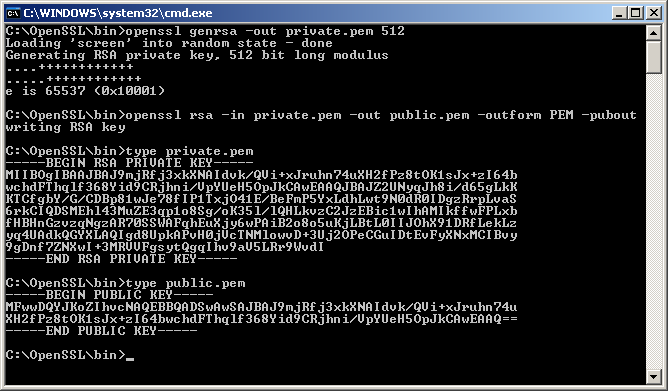
- To generate private (d,n) key using openssl you can use the following command: openssl genrsa -out private.pem 1024 To generate public (e,n) key from the private key using openssl you can use the following command: openssl rsa -in private.pem -out public.pem -pubout.
- The JOSE standard recommends a minimum RSA key size of 2048 bits. To generate a 2048-bit RSA private + public key pair for use in RSxxx and PSxxx signatures: openssl genrsa 2048 -out rsa-2048bit-key-pair.pem Elliptic Curve keys. To generate an EC key pair the curve designation must be specified. Note that JOSE ESxxx signatures require P-256, P-384 and P-521 curves (see their corresponding OpenSSL identifiers below).
The JOSE standard recommends a minimum RSA key size of 2048 bits.
To generate a 2048-bit RSA private + public key pair for use in RSxxx and PSxxxsignatures:
Elliptic Curve keys
To generate an EC key pair the curve designation must be specified. Note thatJOSE ESxxx signatures require P-256, P-384 and P-521 curves (see theircorresponding OpenSSL identifiers below).
Elliptic Curve private + public key pair for use with ES256 signatures:
Elliptic Curve private + public key pair for use with ES384 signatures:
Elliptic Curve private + public key pair for use with ES512 signatures:
PEM key parsing in Java
The BouncyCastle library provides a simpleutility to parse PEM-encoded keys in Java, to use them for JWS or JWE later.
For Maven you should include the following BouncyCastle dependencies (where1.52 is the latest stable version as of May 2015):
Example parsing of an PEM-encoded EC key in Java:
Hey you! This post is outdated!
Take a look at a more correct, detailed, and useful one. What’s the advantage? The EVP functions do implicit symmetric encryption for you so you don’t get hung up on the max length limitations of RSA. Plus, it has an AES implementation.
Disclaimer: I am NOT a crypto expert. Don’t take the information here as 100% correct; you should verify it yourself. You are dangerously bad at crypto.
Last month I wrapped up my Alsa Volume Control server project. To test it, I exposed the server to my public Internet connection and within a few hours, my friend was using the lack of authentication to change the volume on my computer from his apartment. It may not be a serious security hole, and funny as it may be, it would certainly be annoying if someone had malicious intentions in mind. The simple solution is just disable the port forward so the server is only accessible via my LAN, but what fun is that? What if I feel like changing my volume from anywhere for whatever stupid reason I may have?! Thus, I needed to add authentication to the server, which means I also a needed a way to encrypt credentials as they went over the network. And so I opened up the OpenSSL documentation to figure out how to encrypt and decrypt simple messages with RSA in C. Here’s a quick summary…
First up, to do anything with RSA we need a public/private key pair. I assume the reader knows the basic theory behind RSA so I won’t go into the math inside a key pair. If you’re interested, here’s a good write-up on the math behind RSA.
256 aes encryption key generator. Here we’re using the RSA_generate_key function to generate an RSA public and private key which is stored in an RSA struct. The key length is the first parameter; in this case, a pretty secure 2048 bit key (don’t go lower than 1024, or 4096 for the paranoid), and the public exponent (again, not I’m not going into the math here), is the second parameter.
So we have our key pair. Cool. So how do we encrypt something with it?
Rsa Generate Key Code Openssl Update
The first thing you’ll notice is that the message length is limited to 2048 bits or 256 bytes, which is also our key size. A limitation of RSA is that you cannot encrypt anything longer than the key size, which is 2048 bits in this case. Since we’re reading in chars, which are 1 byte and 2048bits translates to 256 bytes, the theoretical max length of our message is 256 characters long including the null terminator. In practice, this number is going to be slightly less because of the padding the encrypt function tacks on at the end. Through trial and error, I found this number to be around 214 characters for a 2048 bit key.
So we have the message. Let’s encrypt it! We allocate memory for a buffer to store our encrypted message in (encrypt). We can determine the max length of the encrypted message via the RSA_size function. We also allocate some memory for an error buffer, in case there’s a problem encrypting the message like if the message is over the practical max length of a message (~214 bytes). From here, all we have to do is call the RSA_public_encrypt function and let it do it’s magic. We supply the number of bytes to encrypt, the message to encrypt, the buffer to put the encrypted message, they keypair to encrypt with, and finally, the type of padding to use for the message. The padding is where the discrepancy between the theoretical length and practical length comes from. The different types can be found on the documentation page for the RSA_public_encrypt function, but the one used above is the one that should be used for new implementations of RSA.
RSA_public_encrypt will return the number of bytes encrypted, or -1 on failure. If -1 we use the OpenSSL error functions to get a more descriptive error, and print it. The error functions are pretty self-explanatory if you read their documentation, so I won’t go into them here. Another sanity check that I didn’t check for would be to ensure that the number of bytes encrypted returned by RSA_public_encrypt is the key size divided by 8, or 256 in this case. If it isn’t, something isn’t right.
Now let’s decrypt the message! Good news is that if you understood the encryption, decryption is very similar.
We allocate the length of our encrypted message to store the decrypted message in. The decrypted message may only be a few characters long, but we don’t know how it’s exact length prior to decryption, so we allocate the upper bound of its length to avoid any length issues. From here, decryption is a simple call to RSA_private_decrypt with the encrypted length, the encrypted message, the buffer to store the decrypted message in, the key to perform decryption with, and the padding type–all very similar to the encrypt function. RSA_public_decrypt returns -1 on error and we check for errors the same way as the encrypt function.
And that’s it! You can now encrypt and decrypt messages with RSA!
But let’s get a little closer to having something that’s actually useful. Let’s see if we can write our encrypted message to a file, read it back, and then decrypt it.
Writing to a file is actually pretty easy. The one caveat to remember is that we aren’t dealing with plain text anymore–we’re working with binary data now so the usual ways to write to a file like fputs aren’t going to work here. Instead, we utilize fwrite which is going to write the encrypted message buffer to the file verbatim. We should check for errors here, but this is just a quick proof-of-concept.
Reading it back is also just as trivial.
We free’d our encrypted message buffer after writing it to the file above as a proof-of-concept above so we need to allocate memory for it again. After that, remember that this data isn’t plain text so the usual fgets isn’t going to work. We need to use fread which will put the encrypted message back into the encrypt buffer which we can then use to send to the decrypt function above.
Let’s also make sure that the data we wrote the file is really there by firing up a terminal and looking at an od dump of the file we wrote.
Here we can see why the file can’t be read as a regular text file. Some of the values are outside of the range of regular characters! Compare this to the plain text of the message that’s encrypted above (hint: it’s “hello”):
Another thing we can do is separate the key pair into a public key and a private key, because what good does sending both the private and public key to decrypt a message to someone do? Let’s revisit the original code we used to generate the key pair.
We generate the key pair as before (this time with a generalized key length and public exponent), but now we used BIO structs to separate the public and private key. BIO’s are just an OpenSSL abstraction to make our lives easier. We use the PEM_write_bio_RSAPrivateKey function and it’s public key counterpart to copy the private and public keys into the newly created BIO structs. We then use the BIO_pending function to get how long our plain text character strings need to be to store the keys and allocate that amount of memory. From there, BIO_read copies the keys from the BIO structs into the character strings. Finally, let’s print them out for fun. Here’s an example of a key pair I generated via this method:
Rsa Generate Key Code Openssl Pdf
So that’s a lot of code! Let’s put it all together into one complete example:
Openssl Generate Rsa Certificate
To compile it (with debug symbols in case you want to debug it), make sure you have the OpenSSL library installed (libcrypto), and then run:
Openssl Generate Rsa Private Key
And there you have it, simple RSA encryption and decryption. I’ll be writing more posts as I further implement this into my Alsa server project on the topics on sending the public key over the network, sending arbitrary size messages with the help of a symmetric cipher (probably AES), doing authentication with Unix users, and doing all this on Android.



